多層濾鏡

通常情況下每一個卷積層都包含多個濾鏡（或稱卷積核），每個濾鏡有其特定的功能或是專精的地方，可能擅長辨識某一類特徵。例如，某些濾鏡可能對垂直線條非常敏感，而其他濾鏡則對輪廓明暗或顏色變化更敏感。當這些濾鏡一起處理同一張輸入圖像時，卷積運算會將它們各自擅長的特徵部分提取出來。每個濾鏡都是一個小的二維矩陣，它在輸入圖像上滑動，並對圖像進行卷積運算，以產生一個2D陣列，我們稱之為特徵圖（Feature Map）。

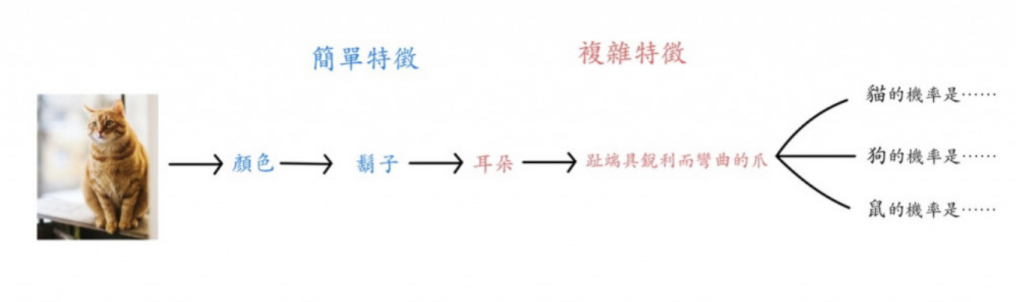
⬆️回憶我們第一天出現過的圖片

深度軸的維度就等於濾鏡的數量

每個濾鏡都會輸出一個 2D 陣列的特徵圖 (也有人把它叫做slice)，把這些濾鏡產生的特徵圖堆起來，就會多出一個深度軸，深度軸的維度取決於使用了多少個濾鏡。最終卷積層輸出的特徵圖就會是個 3D 陣列。（我自己是想成 2D 特徵圖有長跟寬，一張一張疊起來就有高了變成 3D）

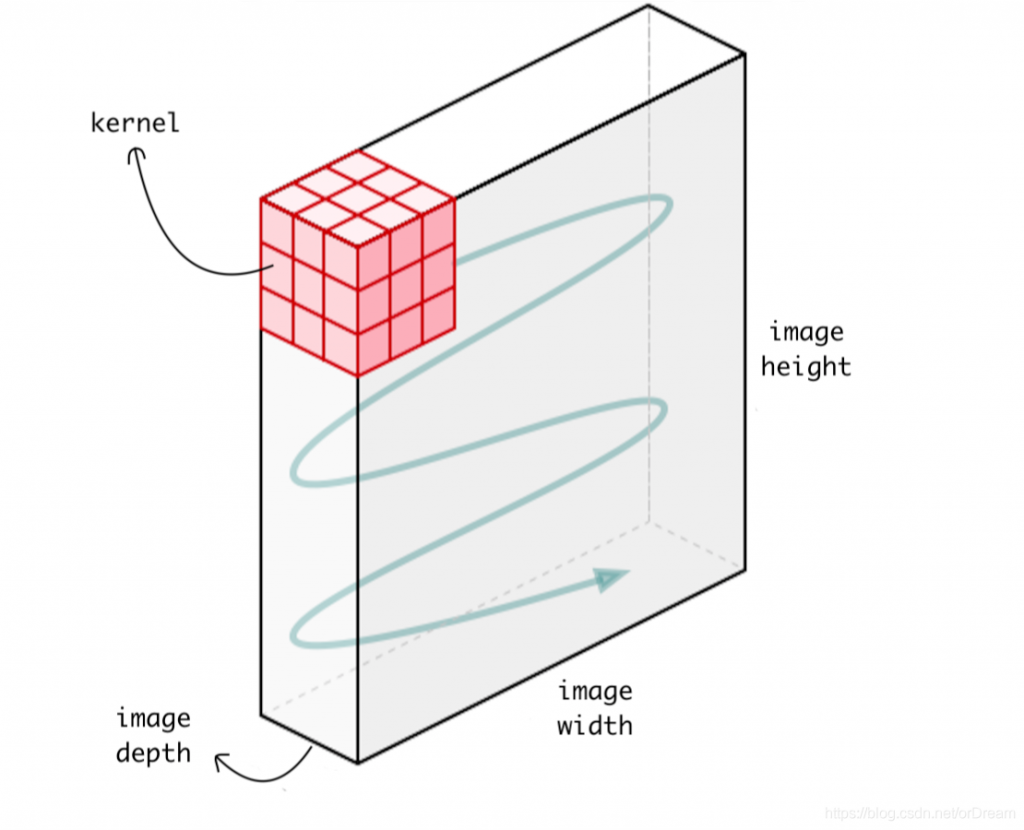
資料來源：https://blog.csdn.net/orDream/article/details/106342711

卷積層的濾鏡數量

我們可以自己決定每個卷積層中應該有多少個濾鏡。這是一個超參數（hyperparameter），它跟密集層要設幾個神經元一樣都是超參數 (super parameter)，下面有些建議 :
(1)濾鏡數量越多越能識別複雜特徵，但需要的計算量也越大。
(2)若神經網路含有多個卷積層，越後面的卷積層所用的濾鏡要越多。因為前面的卷積層主要用於捕捉低層級的特徵，例如邊緣、顏色變化等，而隨著層次的深入，需要更多的濾鏡來捕捉更高層級的特徵，如紋理、形狀、物體部分等。
(3)濾鏡越多計算量越大，故濾鏡數量能少則少。若損失值（val_loss）不會因濾鏡減半（64→32、32→16）而增加，那就可以減少濾鏡的使用。

卷積核的超參數:

(1)濾鏡的尺寸 (常見大小 3 * 3 或 5 * 5) 太大抓太多特徵難以有效學習，太小抓不到特徵不好優化學習
(2)滑動窗口的步長 (stride, 通常是 1 或 2 個像素)太大容易跳過重要特徵
(3)填補 (padding)步長與填補緊密相關，這邊舉一個簡單例子：
首先我們先記得卷積操作的輸出公式:
輸出大小（output size） = [(輸入大小 - 卷積核大小 + 2 * 填充) / 步幅] + 1

接下來假設有一個輸入圖像，大小為6x6像素，並對它進行一次2x2大小的卷積操作，假設：

1. 無填補，步長為1：

   • 如果不進行填補，並且步長設為1，那麼卷積核將在輸入圖像上移動，每次移動一個像素。
   • 在這種情況下，卷積操作的輸出大小為 [(6 - 2 + 2 * 0)/ 1] + 1 x [(6 - 2 + 2 * 0)/ 1] + 1 = 5x5 像素。也就是說，輸出大小比輸入小了。

2. 使用填補，步長為1：

   • 如果使用填補，例如將輸入圖像四周都填補一個像素，然後將步長設置為1，那麼卷積核將仍然在輸入圖像上移動，每次移動一個像素。
   • 由於填補，卷積操作的輸出大小保持與輸入相同，即6x6像素。

3. 使用填補，步長為2：

   • 如果使用填補一個像素，並將步長設置為2，那麼卷積核將每次跨越2個像素在輸入圖像上移動。
   • 在這種情況下，卷積操作的輸出大小是 [(6 - 2 + 2 * 1 ) / 2 ]+ 1 = 4x4 像素。

名詞複習

1. 卷積神經網路（Convolutional Neural Network，CNN）： 用於處理和分析圖像數據的深度學習神經網絡。CNN=卷積層+池化層（明天會介紹）+密集神經網路（之前學過的）

2. 卷積層（Convolutional Layer）： CNN 中主要組成的部分，用於進行卷積操作。每個卷積層包含多個卷積核，每個卷積核負責捕捉不同的特徵。

3. 卷積核（Convolutional Kernel）： 也稱為濾鏡（Filter）。它是一個二維矩陣，通過在輸入圖像上滑動並進行卷積操作，以提取圖像中的特徵。

4. 濾鏡（Filter）： 在卷積神經網路中，濾鏡通常是指卷積核。

最後下面有一個八分鐘影片來說明卷積神經網路，有興趣的人可以參考看看